A feedback system is the one which utilizes presently achieved output of the system for causing variation in the applied input signal in order to get the required output. More simply, we can say that the presence of a feedback system allows getting the desired output with continuous comparison from the reference input of the system.
Generally, these systems are used to provide more corrective response, by comparing the achieved output with the applied input.
By the use of feedback in a control system, the system shows less sensitivity to the unwanted internal and external disturbances.
What is Feedback?
We know that in a control system the controller generates the required signal according to input. However, we have already discussed previously, that control systems are majorly classified as:
In an open-loop control system, the present input is independent of the previously generated output. Thus it is clear that here feedback loop is not present, as no signal is fed back to the input for further considerations.
So, this causes the generation of such a system in which there exists a high possibility of achieving such an output that shows deviation from the desired output. Thus in order to have a system that provides a desired output, feedback systems are used.
Basically, a system incorporated with a feedback loop is known as a closed-loop control system. In such a system, a portion of the output is provided back to the input. Further, the generated output is compared with the present input and according to the fluctuation, the controller generates the signal for achieving the desired value.
In the absence of a feedback system, the output and input show non-interdependency. This means that in such a system, the present output does not put any effect on future output values.
As we have already discussed that the use of feedback in a system, reduces the chances of fluctuation in the system parameters due to unwanted disturbances. This is so because, with variable conditions, the parameters of the system may show variations.
And such variations can lead to cause adverse effects on the performance of the system. Thus the feedback is incorporated in the system, in order to make it insensitive to unwanted changes in the parameter.
Majorly electronics circuits like amplifiers, oscillators, etc. find applications of the feedback systems.
Block Diagram of Feedback System
The figure here shows the block diagram of the control system with feedback:
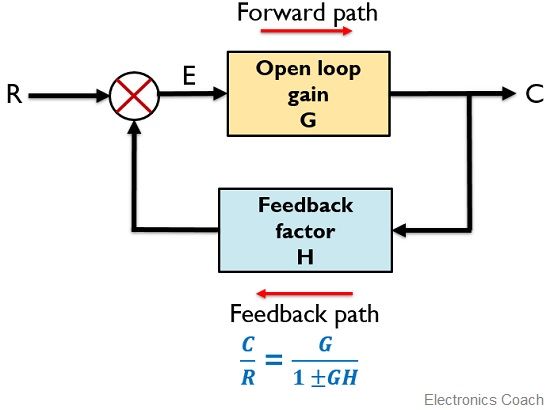
The major concerning factors of a feedback system include sensing, controlling and actuating the process inside the system. More specifically, the reasons for implementing feedback in any electronic circuit are as follows:
- Feedback controls the gain as well as the response of the system.
- The use of feedback introduces the independence of the system’s characteristics with the change in operating conditions like applied voltage and variable temperature.
- The non-linearity of the components present in the system leads to cause a great reduction in signal distortion.
Types of Feedback Systems
In any control system, feedback can be provided in majorly two ways. Thus feedback is generally classified as:
- Positive Feedback: A positive feedback system is the one in which the feedback signal is in phase with the reference input signal. Thus the two get added and combinely the generated response acts as input for further system operation.
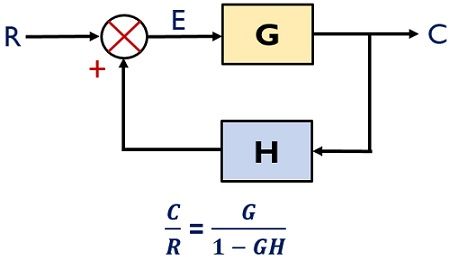
As the two signals get added to give the resultant response in case of a positive feedback system, thus this increases the overall gain of the system.
As the magnitude of the input signal gets increases in case of positive feedback, thereby leading to generate oscillatory response in the system.
- Negative Feedback: The system in which the feedback signal is out of phase with the reference input is known as a negative feedback system. Due to out of phase relationship, the two signals are subtracted in order to produce the difference signal.

The introduction of negative feedback gives rise to a reduction in the overall gain. As the difference in the two values specifies the error value which is needed to be compensated in order to have the desired value. Thus it is always recommended that the system will have a low value of error signal.
As such systems provide better stability and circuit response with an increase in operating bandwidth. Thus most of the control systems utilize negative feedback so as to have a reduction in the overall gain.
For a better understanding of the operation of two types of feedback systems, we can consider an example of a room heater.
When positive feedback is utilized in a room heating system, then when the output temperature is high and it is provided to the reference input then the two will get added and this will lead to cause a further increase in the input signal. Hence the temperature will be raised further above the reference value.
And if the temperature comes below the specified value then it will lead to cause the turning off the system. Therefore, a large category of control system uses negative feedback.
Now let us understand, how the parameters show variation in a control system by incorporating the feedback.
Effects of Parameter Variations on Output
Let us first consider the open-loop control system:
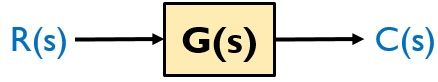
As we know that the transfer function of a system is specified as output by input. Thus for this system, it is given as:
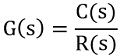
Thus
![]()
Suppose due to variation in parameter, ΔG(s) is the change that gets introduced in the gain, thus the variation in the output will be given as:
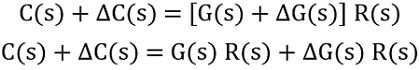
Since we know
![]()
Thus on substituting this in the above equation, we will get
![]()
Hence
![]()
This is the change in output of the system, due to change in the transfer function of the system because of parameter variation in an open-loop control system.
Suppose we have a closed-loop control system:
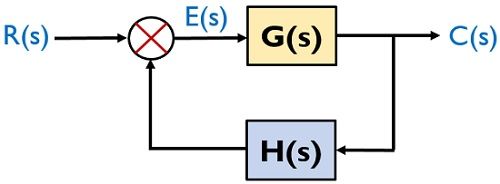
For a closed-loop system with negative feedback, the transfer function is given as:
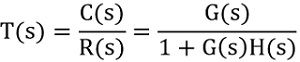
Let ΔG(s) be the change in the transfer function, due to parameter variation, thus the change in output will be given as:
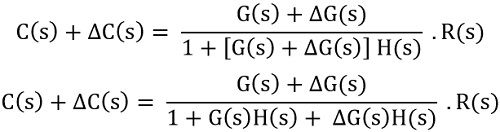
Since ΔG(s)H(s) is very small in comparison to G(s)H(s). Thus it can be neglected from the denominator.
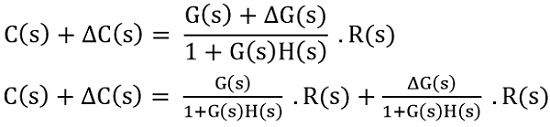
On substituting
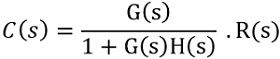
Therefore,
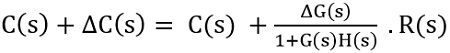
Further
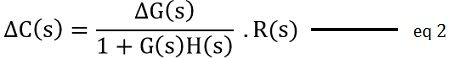
This defines the change in output because of the variation in the parameter.
Since the magnitude value of 1 + G(s)H(s) is quite larger than unity. Thus on comparing eq1 and eq2, it is noticed that due to parameter variation in case of closed-loop system the change is output is reduced by factor 1 + G(s)H(s). This is the outcome of the presence of feedback in the system.
While in the open-loop system, as the feedback is absent thus such a reduction is also absent.
Leave a Reply