Proportional Integral controller sometimes also known as proportional plus integral (PI) controllers. It is a type of controller formed by combining proportional and integral control action. Thus it is named as PI controller.
In the proportional-integral controller, the control action of both proportional, as well as the integral controller, is utilized. This combination of two different controllers produces a more efficient controller which eliminates the disadvantages associated with each one of them.
In this case, the control signal shows proportionality with both the error signal as well as with integral of the error signal. Mathematical representation of proportional plus integral controller is given as:
![]()
The figure below represents the block diagram of the system with PI controller:
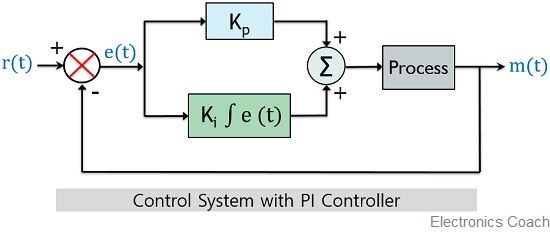
What are Proportional and Integral Controllers?
1. Proportional Controller
Proportional controllers are referred as the type of controllers in which the output signal shows proportionality with the error signal. It is given as
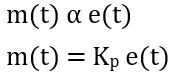
2. Integral Controller
Integral controllers are the type of controllers where the output is proportional to the integral of the error signal. Thus is given as
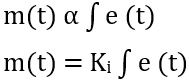
It is to be noted here that one can use integral controllers separately without combining it with proportional controllers. However, generally proportional plus integral controllers are used that combinely overcome the disadvantage of integral controllers.
A major disadvantage which is associated with the integral controller is that these are quite unstable. The reason behind this is that integral controllers show somewhat slow response towards the produced error.
However, the major advantage concerning the proportional controller is that these are designed in a way by which steady-state error gets reduced significantly thereby making the system more stable.
This is the reason the two are combinedly used to produce a type of controller which provides highly stable results.
Proportional Integral Controller
Till now we have discussed what is proportional and integral controller individually. So, let us now understand how the two are combined.
So, in this, the control signal is formed by merging error and integral of the error signal.
Thus is given as:
![]()
We can write it as
![]()
In order to have the transfer function of the controller, we need to consider the Laplace transform of the above equation, so it is given as
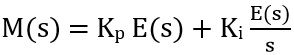
Taking the common term i.e., E(s) out, we will get
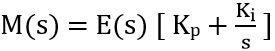
It is to be noted here that the error signal will act as input that will cause variation in the output of the controller.
Thus on transposing E(s) to the LHS, we will get
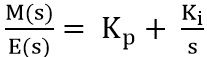
On further simplification, we will get
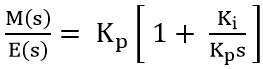
Thus it can be written as:
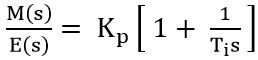
This equation represents the gain of the PI controller.
: Ti = Kp / Ki
So, the block diagram of a PI controller is given as:
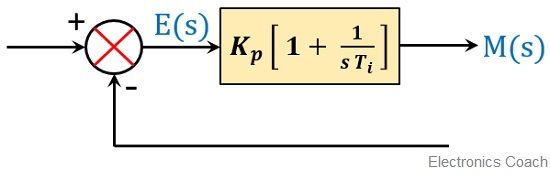
Effects of PI Controller
To understand the effect of PI controller, consider the PI controller with unity negative feedback given below:
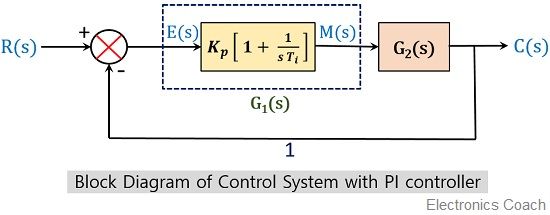
Suppose the gain of the controller is given as G1(s) whose value we have recently evaluated as:
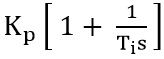
And let the open-loop gain of the system be G2(s), given as
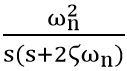
But the overall loop gain of the system will be
![]()
So, on substituting,
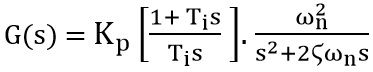
We know that the gain of the closed-loop system or overall controller is given as:
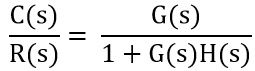
Since we have already considered the unity feedback system.
Therefore, H(s) = 1
Thus the gain will be given as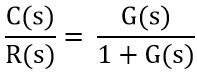
On substituting the values we will get,
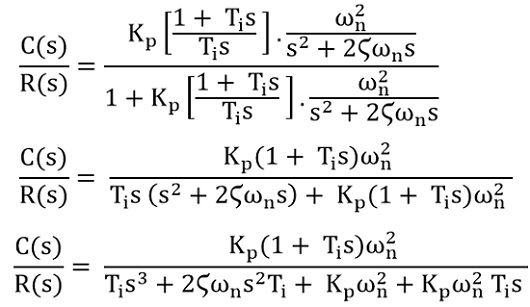
Taking Ti out from the denominator, we will get
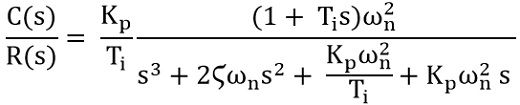
Since we know
Ti = Kp / Ki
So substituting Kp/Ti as Ki in above equation we will get
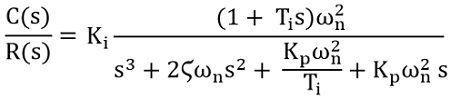
We have already discussed that PI controllers are designed to decrease the steady-state error. And in order to cause a reduction in steady-state error, the type number must be increased. It is to be noted here that the type number of the controller is defined by the presence of ‘s’ in the transfer function.
The above equation clearly indicates that the power of ‘s’ is showing a significant increase in the transfer function. This implies the rise in the type number which resultantly causes a reduction in steady-state error.
When the PI controller is not present in the control system then there will be absence of ‘s’ in the numerator which will cause the absence of zeros in the transfer function.
So, we can say by introducing PI controllers in a control system, the steady-state error of the system gets extremely reduced without affecting the stability of the system.
Bangar Raju Raju. Lingampalli says
It is marvelous, no words to explain.
Excellent, Ma’am. Keep it up