The decimal number system comprises of digits from 0-9 i.e. 0, 1, 2, 3, 4, 5, 6, 7, 8 & 9. The base or radix of the decimal number system is 10 because total number of digits available in decimal number system is 10. It doesn’t imply that these 10 digits will represent only 10 quantities, but all the other digits can be expressed with the help of these numbers.
Decimal number system is the most common number system which we use in our daily lives. If we want to deal with digital system and digital circuit we should be acquainted with other number system such as hexadecimal, binary & octal. The reason behind this is that these number systems have certain advantages over decimal number system and octal number system.
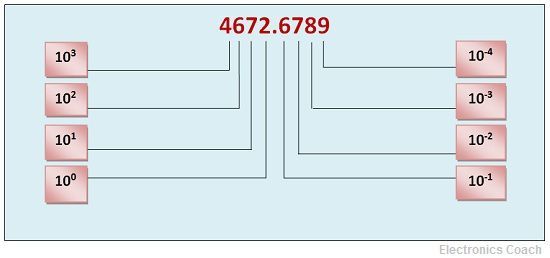
Expansion of Number System
The expansion of the decimal number can be obtained by multiplying each digit of the number with base or radix of the number system i.e. 10, and the base will be raised to the positional value of the digit.

9’s Complement in Decimal Number System
The 9’s complement of a number can be obtained by subtracting every digit of a number by 9. Consider some numbers such as 6, 27, 234, 672 and the 9’s complement of these numbers can be obtained as:-
9-6 = 3, 99-27 = 72, 999-234 = 765, 999-672 = 327, thus 3, 72, 234, 672 are the 9’s complement of the numbers described above.
Significance of 9’s Complement
The procedure of subtraction can be done in much easier steps with the aid of 9’s complement. When we subtract two numbers then we subtract the subtrahend from minuend but with 9’s complement we need not to do subtraction when we are using 9’s complement.
In this procedure we just need to add 9’s complement of the subtrahend to the minuend. When we subtract the smaller number from the larger one, the 9’s complement of subtrahend when added with minuend will result in the formation of carry. We need to add this carry to the result. The resultant addition will be the final answer.
While when we subtract larger number from the smaller one the result of the addition of the subtrahend with minuend will not produce any carry. When addition of 9’s complement doesn’t generate any carry it indicates that the resultant product is negative. The final answer can be obtained by again taking the 9’s complement of this number.

10’s Complement in Decimal Number System
The 10’s complement of the any decimal number can be obtained by adding 1 to the 9’s complement of the same number. Let’ see the steps to find 10’s complement.
- Find the 9’s complement of the number by subtracting every digit of the number from 9.
- The number thus obtained by subtraction will be added with 1.
- Thus, 10’s complement of the number is obtained.
- Therefore, 10’s complement is 9’s complement + 1.
Consider some decimal numbers 7, 34, 566, 3456, now let’s find 9’s complement of each of these.
9-7 = 2, 99-34 = 65, 999-566 = 433, 9999-3456 = 6543
Thus, 2, 65, 433 & 6543 are the 9’s complement of the above considered numbers. Now, in order to find 10’s complement of these numbers let’s add 1 to each of these numbers.
2+1 = 3, 65+1 = 66, 433+1 = 434, 6543+1 = 6544
Thus, 3, 66, 434 & 6544 are the 10’s complement of the numbers 7, 34, 566, 3456 respectively.
Significance of 10’s complement
The 10’s component of the decimal number is crucial in subtracting one number from other. The subtraction can be achieved with the help of addition of 10’s complement of subtrahend with minuend. In this again two cases will arrive which are as follows:-
(i) When a smaller number is to be subtracted with the larger number, in this case one carry will be generated. Ignore this carry and the rest of the digits of the addition will be the answer.
(ii) When a larger number is to be subtracted from the smaller number, in this case the answer will be negative. There will be no carry generation after addition of the 10’s complement of subtrahend with minuend. This indicates that the resultant answer is negative. The final answer can be evaluated by taking the 10’s complement of the number which is obtained after addition of 10’s complement of subtrahend with minuend.

Thus, 9’s complement and 10’s complement are crucial for some arithmetic operations. The decimal system can be extended to the infinite decimal system so that real numbers can also be represented with the help of it. It can be terminating decimal numbers or non-terminating decimal numbers depending on the fact that whether the number is repeating or ending up to a particular value.
These complements are crucial in dealing with the input-output of digital system and microprocessor and micro-controller.
Leave a Reply