Definition: AC bridges are the circuits that are used for the measurement of electrical quantities such as inductance, capacitance, resistance. Along with these an ac bridge allows us to measure storage factor, loss factor, dissipation factor etc. AC bridges operate with only AC signal.
An AC bridge is used to provide phase shifting and providing a feedback path to the oscillator.
AC Bridge network construction
An AC bridge consists of 4 nodes with 4 arms, a source excitation and a balanced detector. Each of the 4 arms of the bridge consists of impedance.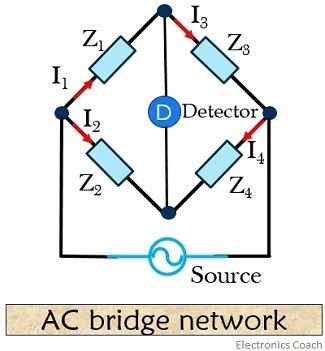
Source and detector in an AC bridge network are connected in opposite nodes. This is so because if source and detector are connected to the same node, all the voltage or current of the source will be displayed at the detector. So, in this condition, the bridge will never come into balance conditions.
Basically, there are 2 conditions in order to balance the bridge-
- The detector current Id should be zero.
- The potential difference between the detector node should be zero.
Now, the question arises what is a balance or null condition in an AC bridge?
It is a condition when certain specific applied circuit situation causes the detector current to become 0.
An AC bridge is a derivative of Wheatstone bridge. This is so because if battery and galvanometer of a Wheatstone bridge are replaced by an ac source and detector respectively. It will behave as an AC bridge.
In case of low-frequency measurements in an AC bridge, the power line may act as the supply source. But, in case of high-frequency measurements, electronics oscillators are used as the supply source.
Headphones, vibration galvanometer and tuneable amplifier are commonly used as detectors in AC bridges.
AC Bridges general balance equation
Let’s now move forward and derive the balanced condition for an AC bridge.
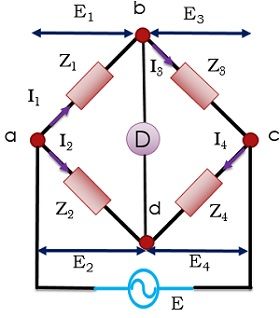
For the bridge to be balanced, considering the above-shown figure
The current through detector must be 0 that requires the potential difference Vbd to be 0.
In such a condition voltage drop from a to b will get equal to voltage drop from a to d, both in magnitude and phase.
So, we can write the above-stated condition as,
E1 = E2
Applying ohms’ law
I1 Z1 = I2 Z2
At balance,
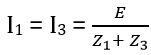
And
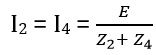
Substituting the value of I1 and I2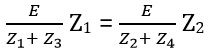

Z1 (Z2 + Z4) = Z2 (Z1 + Z3)
Z1Z2 + Z1Z4 = Z1Z2 + Z2Z3
Hence,
Z1Z4 = Z2Z3
The above equation is the basic equation for a balanced AC bridge. This equation is suitable to use while dealing with a bridge consisting of series elements.
On contrary, while dealing with a bridge consisting of parallel elements, admittances are used. The equation is given as
Y1Y4 = Y2Y3
So, theoretically, we can say that the product of impedances of one pair of opposite arms must equal to the product of impedances of another pair of opposite arms in complex notation.
This means both magnitude and phase angles are to be considered.
Let us now consider impedance in its polar form
Z = Z∠θ
: Z represents the magnitude and
θ represents the phase angle of complex impedance.
The above equation can be written as
(Z1∠θ1) Χ (Z4∠θ4) = (Z2∠θ2) Χ (Z3∠θ3)
: Z1 = (Z1∠θ1)
Z2 = (Z2∠θ2)
Z3 = (Z3∠θ3)
Z4 = (Z4∠θ4)
So, here impedance parameters will get multiplied and angles will be added.
Z1 Z4 ∠ θ1+θ4 = Z2 Z3 ∠ θ2+θ3
Separately we can write magnitude and phase equation as-
Z1 Z4 = Z2 Z3
The condition in above equation is called magnitude criteria and
∠θ1+∠θ4 = ∠θ2+ ∠θ3
This condition is known as phase criteria.
So, in a bridge balance condition, magnitude and phase criteria should be satisfied simultaneously.
Applications of AC Bridges
- AC bridges are used to find unknown impedances along with associated parameters.
- Communication system and complex electronics circuitry majorly make use of AC bridges.
- AC bridge circuits are used in phase shifting and for the filtration of undesirable signals.
- It is also used to measure the frequency of audio signals.
For AC bridge circuits, two balance equations are always obtained. One is the magnitude and the other is phase equation.
Leave a Reply