Definition: Wheatstone bridge is a type of dc bridge that is used for the measurement of unknown resistance. It is a series-parallel combination of 4 resistances that provides zero difference voltage at the balanced condition. The principle of null indication is the basis of working of Wheatstone bridge and thus provides high accuracy in measurements.
It consists of four resistances, out of which 2 are known resistances, one is variable resistance that is used to balance the bridge and another one is unknown resistance whose value is to be measured.
Under the balanced condition, the ratio of the values of two known resistances becomes equivalent to the ratio of the variable resistance and the unknown resistance value. Thus, allows us to calculate the unknown value of the resistance employed in the electrical circuit.
Circuit construction and theory of Wheatstone bridge
The figure below shows the general circuit of the Wheatstone bridge. It consists of 4 arms namely AC, AD, BC and BD each containing resistance R1, R2, R3 and R4. Here, R2 is the variable resistance and R4 is the unknown resistance.
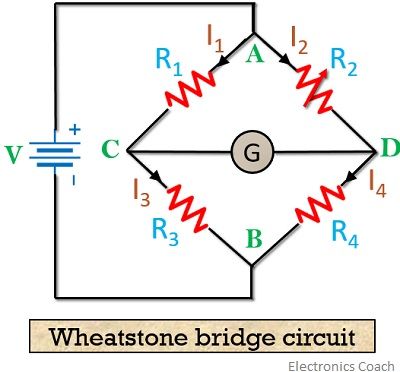
A galvanometer is placed at one arm which detects the flow of current through the circuit on providing the supply voltage at another arm of the circuit.
Let us see how unknown resistance can be calculated in balanced condition of a Wheatstone bridge.
In the absence of any current through the galvanometer, the bridge gets balanced. In other words, the bridge gets balanced when the voltage difference between the two points C and D are equal. Thus, providing 0 voltage across the galvanometer.
In order to determine the bridge balance equation,
![]()
The following condition must be fulfilled in order to have null current through the galvanometer.
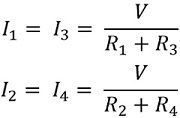
On substituting the above value in previously defined equation
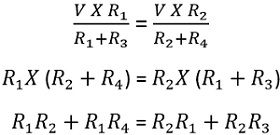
Thus, on cancelling like terms from both the sides, we will have,
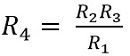
Hence, we can determine the value of unknown resistance in balanced condition using known resistances.
Let’s move further and have a look at 2 separate conditions where the bridge is unbalanced and slightly unbalanced.
Unbalanced condition of a Wheatstone bridge
At the unbalanced condition of the bridge, by applying general circuit analysis we can conclude the extent of deflection. However, Thevenin’s theorem shall be used here.
The figure below shows the unbalanced condition of the Wheatstone bridge.
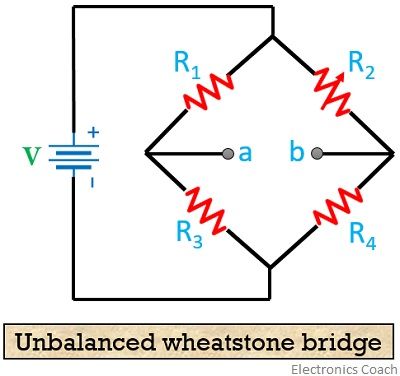
As we can see that galvanometer is not present in the circuit because in Thevenin’s equivalent voltage is determined by detaching the galvanometer. Thus, terminal ‘a’ and ‘b’ are open circuit here in order to find the circuit voltage between the two terminals.
On applying the voltage division equation,
The potential at point a is given as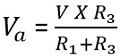
and
The potential at point b is given as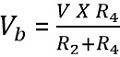
Thus, Thevenin’s equivalent voltage is represented by the potential between a and b which is the difference between Va and Vb
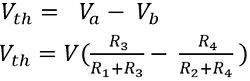
Furthermore, by replacing the voltage source with internal impedance, one can evaluate Thevenin’s equivalent resistance.
As the internal resistance is considered to be very low, we assume it as 0Ω.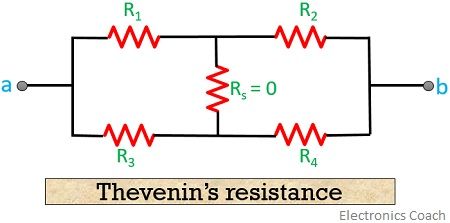
As we can see in the figure shown above that parallel connection of R1 and R3 is serially connected with a parallel connection of R2 and R4.
Thus Thevenin’s equivalent resistance is given as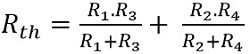
Hence, for the unbalanced bridge circuit, Thevenin’s equivalent circuit is shown below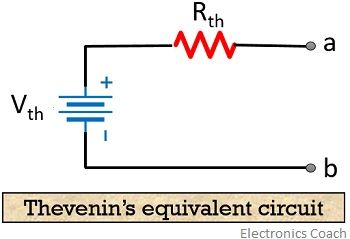
However, by connecting a galvanometer across terminal a and b, the deflection current through galvanometer is given by
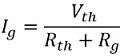
: Rg is the galvanometer resistance
Slightly unbalanced condition of a Wheatstone bridge
In this case, if out of 4, 3 resistances are equal and the fourth one differs by only 5% or less then we can have an approximate expression for Thevenin’s voltage and resistance.
The figure below shows a slightly unbalanced condition of a Wheatstone bridge.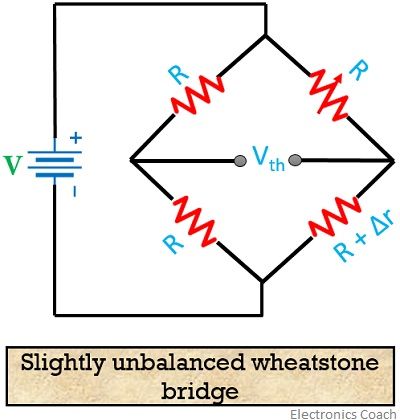
The potential at point a is given as![]()
Similarly, the potential at point b is given as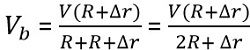
Since Vth is given as the potential difference between points a and b
Therefore,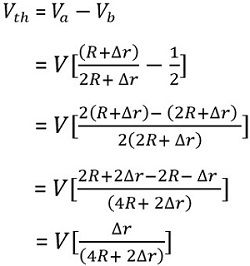
As the value of ∆r is very small in comparison to R, thus it can be neglected.
Hence, Thevenin’s voltage is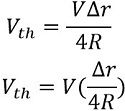
The equivalent resistance is determined when we change the voltage source with its internal impedance.

On neglecting ∆r, Rth is given as![]()
Thevenin’s equivalent for the slightly unbalanced bridge is shown below-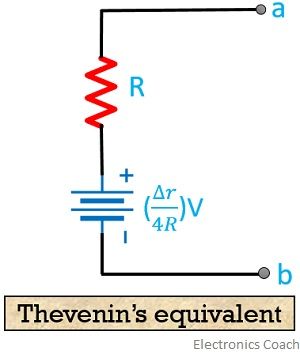
Sensitivity of Wheatstone bridge
The sensitivity of a Wheatstone bridge is defined as the deflection in the galvanometer per unit current. In the unbalanced condition of the bridge, when current flows, it causes the pointer of galvanometer to get deflected. Thus, the deflection rate is the function of sensitivity.
A greater amount of deflection can be noticed for the same current in case of a more sensitive galvanometer. The total deflection D is given as
D = S Χ I
: S is sensitivity and I is current in microamps.
Applications of Wheatstone bridge
- It is used to measure dc resistance.
- Wheatstone bridge is widely used in cable faults identification by telephone companies.
- It can measure physical quantities like light, temperature etc when used with an op-amp.
- By some modulation to bridge network, we can calculate capacitance, inductance and impedance.
Limitations of Wheatstone bridge
- In Wheatstone bridge sometimes measurements of low resistance generate erroneous results. Thus, Kelvin’s double bridge was introduced to overcome this.
- It is always preferable to measure medium resistances with Wheatstone bridge as for high resistance measurements it is not suitable. This is so because in case of high resistance the galvanometer is not sensitive to imbalance.
- The heating effect due to the current in the circuit unnecessarily changes the resistances employed in it. This sometimes causes a permanent change in resistance due to a large current in the circuit.
Thus, from the above discussion, we can conclude that dc bridges that operate on dc supply allow us to determine the unknown resistance. However, an ac bridge allows us to measure resistance, inductance and capacitance when fed with an ac source.
Leave a Reply