Methods of Sweep Voltage Generation

As we are aware of the fact that a time base generator does not provide accurate linearity in sweep voltages. Thus various methods of Sweep Voltage Generation are used in order to have a linear output.

The methods are discussed below:

Exponential sweep circuit

The circuit of a basic sawtooth voltage generator is shown below: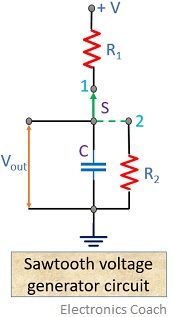

In the circuit, the position of switch S changes from 1 to 2 thus causing the capacitor to be charged and discharged alternately. Thus an output is achieved that is shown below:

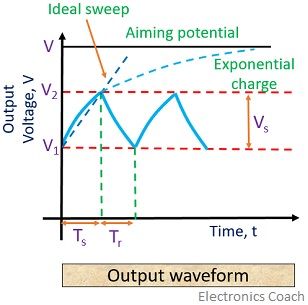
Here, T_s and T_r are the sweep and retrace time respectively. The display systems require to retrace time so that the started beam can return to its initial position before the beginning of the next cycle.

When the switch is at position 1, the capacitor charges with the supply voltage V. But, before it is fully charged the switch changes its position to 2 that causes the capacitor to discharge until the switch does not return to position 1 again. Thus we can have an output as shown above. The supply voltage potential is also termed as aiming potential.

The voltage at the output is given by:

and

When t = T_s, V_out (T_s) = V₂

Furthermore, at t = T_r, V_out(T_r) = V₁

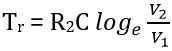
V_s is the sweep amplitude and is given by

As we can see in the waveform that the straight line and exponential charges are nearly identical in case of a smaller value of V₂. So, in order to achieve better linearity, the sweep voltage must be a small portion of a supply voltage.

Now, moving further let us consider, switching circuit comprising of a UJT.

Here, the capacitor employed in the circuit is charged through resistor R_e when V_BB is in on state.

At the time of capacitor charging, there is an exponential increase in the voltage across the capacitor before attaining peak potential V_p. As the capacitor attains peak value during charging, the UJT switches on that cause the capacitor to discharge quickly via B₁. When the voltage across R increases, the voltage across the capacitor drops to V_v. This causes the device to cut off and again the charging of the capacitor starts. In this way, a continuous process generates a sawtooth waveform and the resulting waveform is shown below.

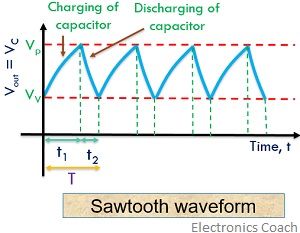
As the time constant is dependent on resistor R_e. So, the frequency of the output can be varied according to the variation in R_e. In normal conditions, t₂ is very much less than t₁ and can be neglected for approximate calculations.

At the time of charging, the capacitor voltage is given by,

: R_eC= τ i.e., the time constant

As we know, after the charging period, when V_p becomes equal to V_c the capacitor starts to discharge.

It can be written as,

 

when V_B is neglected.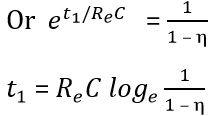

Therefore, the charging period,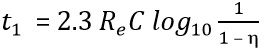

Seeing that, discharging time is small as compared to charging time.

Hence, T = t₁

The time period of the wave is given as,

And the frequency of oscillation is given as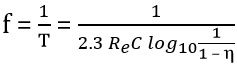

Turn ON and OFF condition of a UJT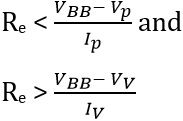

So, we can write,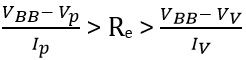

Bootstrap time base generator

In this category in order to maintain a constant current, bootstrapping is done.

What is bootstrapping?

It is basically a process in which by using a feedback system, some part of the output is given back to the input, thereby increasing or decreasing the input impedance of the circuit.

As we can see in the figure shown below:

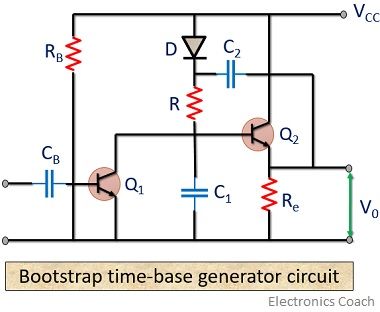
It consists of two transistors Q₁ and Q₂ along with a diode D. The anode side of the diode is connected to V_CC and the cathode side is connected to the output capacitor C₂. The output voltage is observed as the voltage across capacitor C₁ employed in the circuit.

Operation:

At time t = 0, V_cc drives the circuit, that turns on Q₁. The capacitor C₂ employed in the circuit is charged to V_cc through the diode. A negative trigger pulse applied at the base of Q₁ turns it off. This causes C₂ to discharge and now C₁ starts charging. Due to large capacitance value, C₂ discharges slowly thereby maintaining a constant value.

Now, the diode D is reverse biased at ramp time. A small amount of current is provided by C₂ to C₁ in order to charge it. At the end of ramp time when Q₁ gets on, the charged capacitor C₁ now discharges and the voltage appears across the output. Again when D gets forward biased C₂ recovers its charge lost at the time of charging C₁. Thus the circuit produces a ramp output that is shown below:

Miller sweep generator

It is also known as miller integrator that generates a sweep waveform. The initial stage of a miller circuit comprised of a switch along with a timing circuit as shown in the figure below:

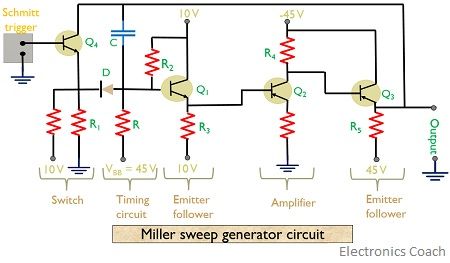
The rest part of the circuit serves as an amplifier section and emitter follower section works as a buffer amplifier having high input impedance and low output impedance. This resultantly provides higher amplifier gain. The sweep speed of the generator varies with the variation in R, C and V_BB.

Operation:

Here, transistor Q₄ turns on by the application of the negative pulse from the output of the Schmitt trigger. Thus current flows through resistor R₁. This negative potential forward biases the diode in the circuit but as C is the bypass capacitor here so it will not be charged.

When the trigger is applied, it causes Q₄ to turn off. The switch employed in the circuit applies a potential of 10 V that causes current to flow through R₁ thus making the diode reverse biased. The applied V_BB potential now charges the capacitor through resistor R and generates a sweep signal at the output. At the end of the sweep, the capacitor discharges through D and Q₄.