Relaxation Oscillator

Definition: A relaxation oscillator is basically a non-linear oscillator that has the ability to generate a non-sinusoidal periodic waveform at its output. Such as triangular wave, square wave etc. These are also known as non-sinusoidal waveform generators.

A relaxation oscillator operates in such a way that it generates oscillations by charging the capacitor and quickly discharging it after attaining a pre-determined threshold voltage.

The figure below will help you to understand the conceptual idea of the relaxation oscillator:

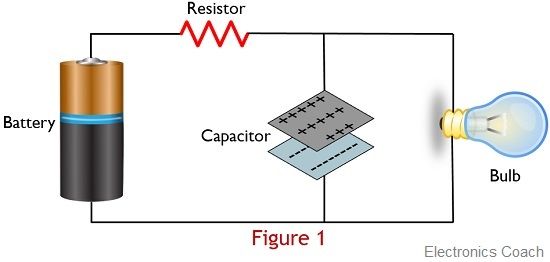
Here we can see a capacitor is placed that stores the energy supplied by the external source in one phase and releases that particular energy in another phase.

Basically, at the time of charging of the capacitor, the bulb connected to the circuit does not get illuminated. But at the time of discharging of the capacitor, the bulb starts flashing for a time period determined by the RC time constant.

This operating principle is adopted by the relaxation oscillator.

In this section, we will discuss UJT relaxation oscillator that uses a unijunction transistor in its circuit. And an op-amp relaxation oscillator that generates a square wave at its output.

UJT Relaxation Oscillator

The figure below represents the basic circuit diagram of UJT relaxation oscillator:

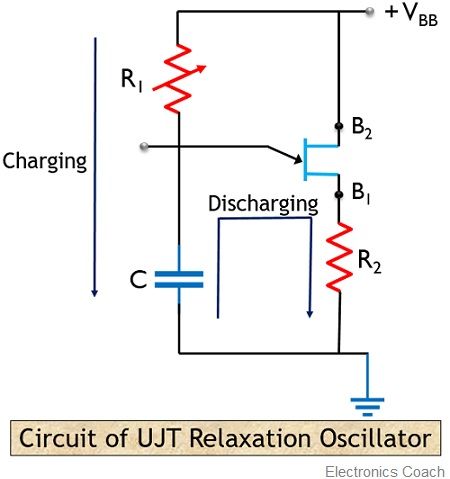
Here we can clearly see that the circuit is composed of a unijunction transistor and a capacitor which gets charged through resistor R₁ and gets discharged through resistor R₂.

The externally supplied voltage to the circuit is V_BB.

Let us now move further to understand how a UJT relaxation oscillator provides a non-sinusoidal waveform at its output.

When the interbase supply voltage V_BB is supplied to the circuit. Then the capacitor present in the circuit starts charging through resistor R₁. At the time of charging of the capacitor, the voltage present across the capacitor shows an exponential increase until a peak voltage is achieved. This peak voltage is indicated as V_p.

Once the capacitor voltage reaches V_p, the UJT present in the circuit gets on. And as the UJT turns on, the capacitor now starts discharging through the resistor R₂ present in the circuit.

So, the discharging current flowing through the resistor R₂ generates a voltage spike.

The figure below represents the voltage waveforms across the capacitor C and resistor R₂:

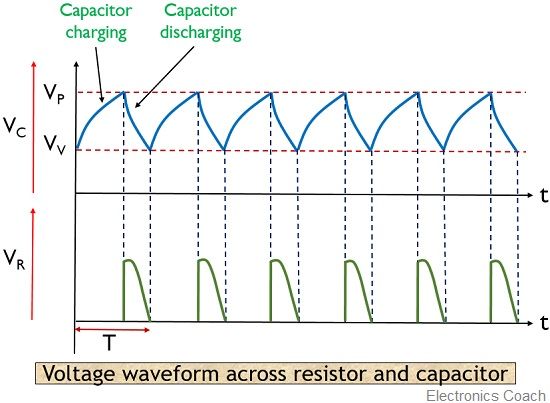
At the time of the capacitor discharging the voltage across it drops to V_V. Thereby cutting off the device. Once the cut off state is reached, the capacitor again starts charging thereby causing the repetitive cycle to take place.

This repetitive cycle of charging and discharging of the capacitor produces sawtooth waveform across it.

It is to be noted here that when UJT is off, the output voltage will be 0. As at this particular interval the applied voltage charges the capacitor hence output voltage will be zero.

Due to this relaxing state of the oscillator, it is termed as the relaxation oscillator.

So, the frequency of oscillations of the oscillator relies on the charging and discharging of the capacitor.

Op-amp Relaxation Oscillator

An op-amp relaxation oscillator is basically a square wave generator. Here also the frequency of oscillations is determined by the charging and discharging of the capacitor.

The figure below represents the op-amp relaxation oscillator:

The circuit generates a square wave at its output. As we can see that the circuit is composed of a capacitor, an op-amp, resistors and 2 zener diodes.

Here, the op-amp comparator utilizes positive feedback in order to increase the amplifier gain. The high gain of the op-amp causes the output of the op-amp to switch rapidly between one level to another.

The positive feedback provided to the op-amp fed some part of the output to the non-inverting input terminal.

Also, the capacitor voltage V_c is provided to the inverting terminal of the op-amp.

The input voltage V_in is given as

V_in = V_c – β V_out

When an input voltage V_in is positive then the output voltage will be V_out = -V_Z1 while when the input voltage V_in is negative then the output voltage will be V_out = +V_Z2.

Let for a particular time the input at the terminal of the op-amp is negative or less than 0. So, in this case, the output generated will be V_out = +V_Z2. This causes the voltage at the non-inverting input terminal to be β V_Z2.

Hence the capacitor starts charging exponentially with V_Z2. Till the time V_C is equal to β V_Z2, the voltage at the output will remain at V_Z2. Now, the output of the comparator gets reversed to -V_Z1. This causes the charging of the capacitor with -V_Z1. Thereby causing the transition from -V_Z1 to +V_Z2.

So, here also, the charging and discharging phenomenon of the capacitor determines the time period of the output waveform.

The figure below shows the output and capacitor voltage waveform for op-amp relaxation oscillator:

The circuit of op-amp relaxation oscillator is also known as an astable multivibrator, as the circuit holds 2 quasi-stable states. Hence, the signal performs the transition between 2 states. Thereby generating the square wave signal at the output.

Applications of Relaxation Oscillator

These are used to produce internal clock signalling in any digital circuits. These also find applications in thyristor triggering circuits, in oscilloscopes as well as television receivers etc.