State Space analysis (also known as state variable analysis) is a commonly used method nowadays for analyzing the control system. The analysis that involves providing a complete idea about the behavior of the system at any given time utilizing the history of the system is known as state-space analysis.
The analysis of the control system in this approach is based on the state of the system. Thus it is called so.
We know that the basic method used to analyze the control system is a transfer function approach. This means that conventionally, the transfer function approach was utilized for analyzing the system.
And the transfer function of the system is specified in terms of the ratio of frequency domain representation of output to that of input.
Need for State Space Analysis
Despite having a transfer function approach why do we need state-space analysis?
The conventional method was easy to apply in order to analyze the system but at the same time, there were some major drawbacks associated with it.
The drawbacks associated with the conventional method are as follows:
- In the transfer function approach during analysis, the initial conditions are considered to be 0. However, this is not the case with state variable analysis because it considers all the initial conditions associated with the elements of the control system.
And the consideration of initial conditions provides a more precise response. Hence the consideration of all the initial conditions associated with the system in the state model serves as a major advantageous factor. - The transfer function approach shows inconvenience towards the analysis of multiple input multiple output systems. As against the state variable approach supports analyzing both SISO as well as MIMO systems.
- Due to the effectiveness in analyzing linear and non-linear as well as time-varying or time-invariant systems, the state-space approach is better than the transfer function approach which is applicable to linear time-invariant systems.
- As the transfer function approach is a frequency domain analysis thus it offers difficulty in finding the time domain solutions in case of a higher-order system. Whereas state space analysis is a time-domain approach.
- The transfer function approach uses some standard test input signals for the analysis of the system, while this is not the case of state-space analysis.
- As the state variable approach is associated with matrix/vector modeling thus is considered as an efficient computational approach. Hence it facilitates accurate response thus is applicable to dynamic systems.
Thus, we can say state-space analysis overcomes the limitations of the transfer function approach.
What is meant by ‘State Space’?
The analysis of the system using conventional methods like root locus or bode plot etc. utilizes the transfer function approach where the system is analyzed on the basis of output and input.
In this approach, the interior conditions of the system are not taken into consideration and are restricted to only a single input single output.
But in the case of a modern approach, brief information on the internal conditions of the system is considered. These internal conditions specify the state of the system. Thus called state space.
What is State?
It represents every smallest past information of the system in order to predict response. Basically a state separates the future i.e., the response of the system from the past.
Thus more simply we can say that to have the accurate response of the system for any given input, the state holds the information related to the history of the system.
Therefore, at any instant of time, the state signifies the combined effect of each element of the system. Hence the state is a vector in nature that provides the values from each component associated with initial conditions of the system.
Due to vector nature, it is generally known as a state vector.
As we have discussed that it is a vector term thus the various variables that constitute state vector are known as state variables.
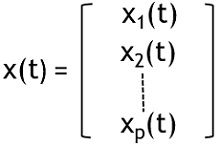
Here x(t) denotes the state vector while x1(t), x2(t), etc. are the state variables that are forming state vector.
State Model
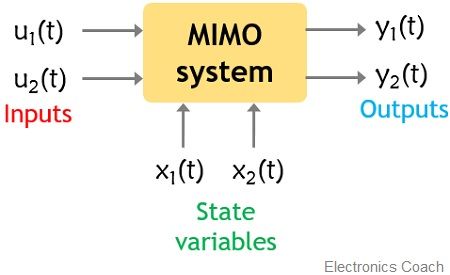
Consider a linear system with two inputs u1(t) and u2(t), while two outputs y1(t) and y2(t).
Suppose the system is having two states x1(t) and x2(t).
- State Equation
We know that state variables show variation with time. Thus writing the differential equation of the state variable, we will have

Thus the matrix representation will be given as:
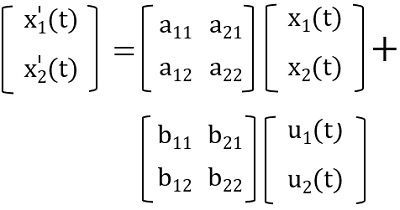
Therefore, the generalized form:
![]()
- Output Equation
The output of the system will be represented as the linear combination of the state of the system and the applied input. Thus is given as:
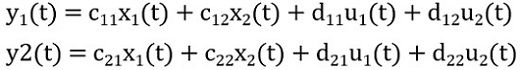
The coefficients c and d taken over here are constants. Thus writing the above equation in the form of a matrix, we will have:
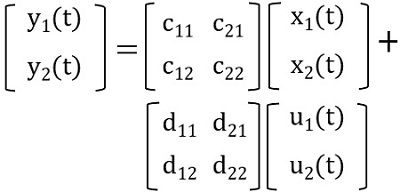
Therefore, in general form, we can write it as:![]()
Thus the two equations combinedly form the state model of the linear system:
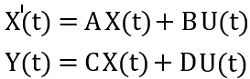
Modeling Procedure
In the state model, we have considered 2 states, 2 inputs and 2 outputs of the linear system. But generally, we can define the complete system model of a linear time-invariant system as:
- A set of state equations defined in the form of matrices A and B, while
- A set of outputs defined using state variables and inputs in the form of matrices C and D.
It is to be noted here that as A and B are the coefficients associated with the state equation, thus are the properties of the system. Therefore, the elements and the structure of the system are responsible for the determination of A and B.
While as C and D are the matrices of output variables thus its determination shows dependency on the output variables.
So, the steps involved in the modeling procedure are as follows:
- Initially determine the order of the system and then select the set of state variables.
- Now, using the proper methodology, define the state equations of the system with matrices A and B.
- Lastly, find the set of output equation thereby deriving C and D matrices.
Disadvantages of State Space Analysis
As we have discussed at the beginning itself that to overcome the disadvantages associated with the conventional approach of analysis, the state-space analysis was introduced. But the major drawbacks concerning state-space analysis involves complex technique and requirement of high computations.
Leave a Reply