Controllability

Controllability is defined as the ability of a control system to reach a definite state from a fixed (initial) state in a finite time. It is considered as an important property of the control system as it defines the behaviour of the control system.

The theory of controllability was proposed in 1960 by R. Kalman.

Controllability in Control System

A system is completely controllable if the initial state of the system is transferred to any particular state, in a finite time duration, when a controlled input is provided to it.

Controllability is considered as one of the basic as well as major concepts of the control system. However, another crucial concept associated with the control system is observability.

We know that the control system is designed to generate the desired output when a reference input is provided to it. But it is obvious that when a system functions then various factors are associated with it that hinder the performance of the system. This is the reason, the chances of getting the desired output on applying specific input get reduced.

However, the closed-loop control system that uses a feedback network facilitates providing the desired output of a control system. We know through a feedback network a part of the output is fed back to the input that is compared with the reference input in order to determine whether the achieved output is accurate or not.

But a closed-loop system must also be properly controllable so as to avoid the failure of the system. As the failure of the system leads to cause environmental disasters along with economical difficulty.

We have already discussed in the state space analysis, that the analysis of a system at any particular time in a control system provides the idea of the behaviour of the system. And for a control system, the determination of the behavioural approach of producing the output is necessary.

A state-space analysis uses the state of the system for the purpose of analysis. Controllability is also majorly associated with the state of the system and sometimes with the output.

This is so because if a state of the system can be changed to another desired state in the presence of reference input in the finite time duration, then such a system is known as a completely controllable system.

Controllability stabilizes an unstable system.

Thus, we can say a dynamic system that does not offer, transferring one state to another is not a controllable system.

As the theory of controllability was proposed by Kalman, thus a test named Kalman’s test is used to determine whether the system is controllable or not.

Kalman’s Test

Suppose we have a linear time-invariant system with n^th order multiple inputs, then the state equation is given as:: A is a matrix of order n*n

X(t) is the state vector of order n*1

U(t) is a vector of order m*1 where m is the number of inputs

Basically, for a control system to state controllable, the necessary condition is that the rank of the composite matrix Q_C is n.

The composite matrix Q_C is given as:

So, in Kalman’s test, the determinant of Q_C is determined. The value of the determinant of Q_C shows whether the system is controllable or not.

If its value is non-zero then this represents that the system is completely controllable.

It is to be noted here that the rank of the composite matrix should be n for the complete state controllability.

Let us take an example to understand this, suppose we have:

Here n = 2

So,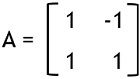

And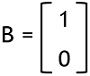

Therefore,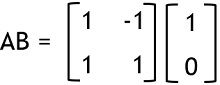

Hence on solving the matrix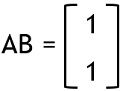

Now composite matrix will be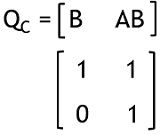

Further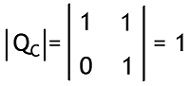

Here determinant of the composite matrix is non-zero.

Also, the rank of Qc i.e., n is 2.

So, the system is of controllable nature.

Consider another state equation: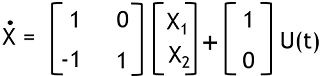

Here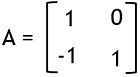 

and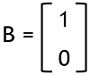

Thus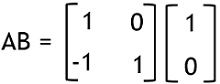

On solving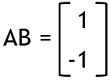

Thus the composite matrix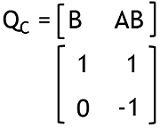

So, the determinant of Q_C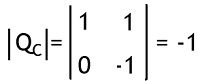

As it is again a non-zero value. So. it’s a controllable system.

Condition for Controllability in s-plane

We know in s-plane, the system is represented using the transfer function. So, in the case of s-plane, the controllability of the system is defined by the transfer itself.

If the numerator and denominator polynomials do not contain a common factor, except the constant term then such a system is said to be controllable. The polynomials of the transfer function are known as coprime.

More simply we can say, the pole-zero of the transfer function should not get cancelled.

Output Controllability

Sometimes, the system must be practically controllable in terms of output variables rather than state variables.

Thus, for a linear time-invariant system with the state model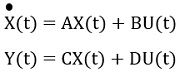

The output controllability of the system is associated with the ability to construct such an unconstrained input vector that can change the initial output to final output in a finite time interval.