Observability of a control system is the ability of the system to determine the internal states of the system by observing the output in a finite time interval when input is provided to the system. It is another crucial property of the control system as it shows the behavioural approach of the control system.
It is also proposed by R. Kalman, the one who proposed controllability.
Observability in control system
For a better understanding of the term observability, let us understand it in terms of a question.
Suppose for the applied input to a control system and if we can measure the output of the system for that particular input in the finite time. Then, can you predict the initial state of the system by having the knowledge of the input and output?
If yes, then the system is observable.
In the previous article, we have studied about controllability. Both controllability and observability are duals of each other. As the two are duals thus it is necessary to give you an idea about controllability.
So, basically, in a control system, controllability is the ability of the system to change the initial state to a definite state by the application of input in a finite amount of time. Contrastingly, observability reverses the procedure by determining the internal states from the achieved output. This facilitates the determination of the behaviour of the system. Therefore, the above discussion concludes, that a system is observable if for a possible sequence of state vectors, with the use of output Y(t), every state is determined completely, in a finite time.
It is noteworthy here that if few of the states are not practically determined then the system is not completely observable.
This shows, that it will lead to providing behavioural characteristics of the overall system from the output of that system.
So, if the system is not observable, then each and every state will not be determined even if the output is known. This somewhat represents that the internal states of the system are itself unknown to the controller.
In order to check whether the system is controllable or not, like the controllability, Kalman’s test is performed.
Kalman’s Test for Observability
The state equation for a linear time-invariant system of nth order is given as:
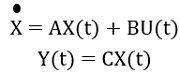
: Y(t) is the output vector of order p*1 and
C is another matrix of order 1 * n
Here according to Kalman, the system is said to be completely observable only under the condition that the rank of the composite matrix is ‘n’.
The composite matrix Qo :
![]()
Here ‘T’ represents the transpose of matrices A and C
Thus, for the above-given composite matrix, the system is said to be completely observable if its rank will be ‘n’.
In Kalman’s test, we need to determine the determinant of the matrix. If its value is not equal to zero then the system falls under the category of observable system.
So, for this, let us take an example to check whether the system is observable or not.

and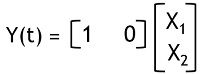
The rank n is 2. So,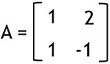
and![]()
So, the transpose matrix will be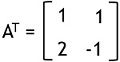
and
We know that the composite matrix is given as:
QO = [ CT : ATCT ]
So,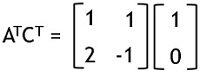
Therefore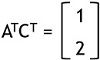
So,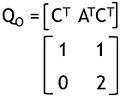
Further,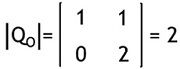
As it is clear that the determinant achieved here is 2, thus is non-zero. Also, the rank here is 2.
So, we can say that this system is completely observable.
Consider another example,
and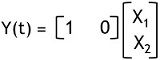
Here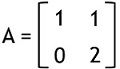
and![]()
Thus, the transpose matrix
and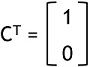
Here we already have CT. So finding ATCT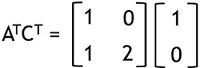
So,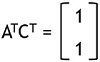
Therefore, the composite matrix will be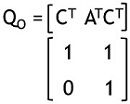
So, the determinant will be
As again the determinant is a non-zero value and also the rank of the matrix is 2.
Thus, the system completely observable.
This signifies that by observing the output of the system, the internal states of the system can be determined.
Condition for Complete Observability in s-plane
In s-plane, the representation of the system is generally done through the transfer function approach. Thus, observability for a system represented in s-plane is determined by its transfer function.
Like the concept of controllability, in observability also, if there must be no common polynomial in numerator and denominator. This signifies pole-zero cancellation must not exist in the transfer function of the system.
The reason behind this is that if the polynomials are not coprime then they will get cancelled and so the observation of the cancelled mode will not be possible at the output.
Hence, with an incomplete output, the system cannot be completely observable.
Bilawu Muritala says
I really enjoy this simple explanation.
Thanks