Routh-Hurwitz Stability Criterion

Routh-Hurwitz stability criterion is an analytical method used for the determination of stability of a linear time-invariant system. The basis of this criterion revolves around simply determining the location of poles of the characteristic equation in either left half or right half of s-plane despite solving the equation.

We have already discussed, the stability of the control system in our previous article. It is considered an important parameter of the control system.

The stability of a control system basically defines its ability to reach the steady-state and remain there till the time, specific input is maintained despite the variation in the other factors associated with the system.

Thus, to check whether the system is stable or not, the conditions of stability criterion must be satisfied.

Routh-Hurwitz Criterion

This stability criterion is known to be an algebraic technique that uses the characteristic equation of the transfer function of the closed-loop control system in order to determine its stability.

According to this criterion, there is a necessary condition and a sufficient condition.

If the necessary condition is not satisfied by the system, then it is said to be an unstable system. However, even after satisfying the necessary condition, the system may or may not be stable.

Therefore, we need sufficient condition to determine whether the system is stable or not.

Suppose the transfer function of the closed-loop system is given as:

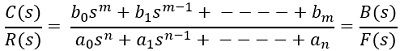
: a and b are the two constants here.

On equating F(s) = 0, we will get the closed-loop poles of the system, which is known as the characteristic equation of the system, given as:

Moreover, the roots of this characteristic equation are the poles of the system with the help of which the stability of the system is decided.

It is to be noted here that before checking the stability of the system using the Routh-Hurwitz criterion, a basic analysis must be done.

This general test is simply done by analyzing the characteristic equation, here all the roots of the equation must be present on the left side of the s-plane.

The necessary conditions are discussed below:

• The coefficients of all the polynomials of the equation should be of a similar sign.
• Also, all the coefficients must be present, this means that any of the power of ‘s’ from ‘n’ to 0 must not be absent.

These two are not sufficient conditions to prove the stability of the system.

Initially, the sufficient condition to have the poles in the left half of s-plane was proposed by Hurwitz. It was known as Hurwitz criterion and states that all the subdeterminants of the Hurwitz’s determinant must be positive.

However, some disadvantages were associated with that particular method. The disadvantages are as follows:

• Solving the determinants of the higher-order system is quite difficult and time-consuming.
• In the case of an unstable system, the number of roots in the right half of s-plane is non-determinable by this method.
• The prediction of marginal stability is not easy.

So, because of these disadvantages, Routh proposed another technique for determining the stability of the system, this method is generally known as the Routh-Hurwitz criterion or Routh’s criterion.

Hence, according to Routh, for a stable system the necessary and sufficient condition is that in a routh array, all the terms that are present in the first column must be of the similar sign. This means no change of sign (either from positive to negative or negative to positive) must exist in the first column of the array.

Therefore, in case if there is any sign change then such a system becomes unstable.

This is said on the basis that the overall sign changes in the first column signify the total number of roots lying on the right half of the s-plane, thereby making the system unstable.

Thus, in simple words, we can say, that for a system to be stable, each coefficient of the first column of the array must have a positive sign. If it is not so, then it is an unstable system. And the number of sign change that makes the system unstable shows the number of poles that are present on the right side of the s-plane.

This is known as the Routh-Hurwitz Criterion.

What is Routh Array?

Till now we have used the term coefficients of routh array so many times. But the basic question is what is routh array and how it is formed.

Basically, under the Routh-Hurwitz stability criterion, Routh proposed a technique by which the coefficients of the characteristic equation are arranged in a specific manner. This arrangement of the coefficients forms an array which is known as routh array.

Let us now see how a routh array is formed. Consider the general characteristic equation:

For the routh array, the first two rows are written from the characteristic equation directly while the rest of the rows are formed with the help of previous rows.

It is to be noted here that if in the characteristic equation, n is odd then the first row of the array will hold the odd coefficients. While if n is even then there will be even coefficients present in the first row.

In this way, the first and second row of the array will get formed. Let us now see how the rest of the rows will get formed.

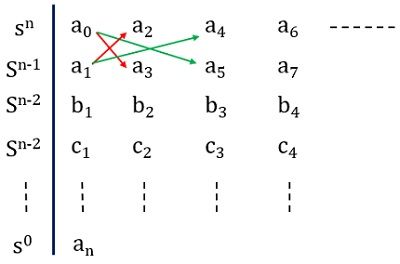
So, the third row will be formed using the first and second rows. Let us see how

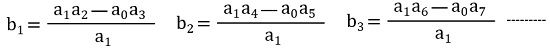
In a similar way after forming the 3^rd row, we can use 2^nd and 3^rd row to form the 4^th row

and so on.

Therefore, we have to continue the process until the time we get the coefficients for s⁰, which is nothing but aⁿ. In this way, we get routh array from which the stability of the system is predicted.

Now there are two special cases that cause the failure of the Routh’s test:

• Case 1: If in any of the rows the first element is 0 and in the same row even a single non zero element is there then in the next row there will be an infinite term and this will lead to failure of Routh’s test.
• Case 2: If there is such a row in routh array whose all the elements are 0 then it will be impossible to determine the next row and thus the Routh’s test fails in this condition also. This is so because the presence of only 0 in a row shows the absence of coefficients in that particular row.

Advantages of Routh-Hurwitz Stability Criterion

1. It offers an easy method of predicting the system’s stability without completely solving the characteristic equation.
2. In case, the system is unstable then we can easily get the number of roots of the characteristic equation that has a positive real part.
3. The time to calculate determinants is saved by the Routh-Hurwitz criterion.
4. By using this we can get the range of values of K.
5. It provides ease of determining the relative stability of the system.

Disadvantages of Routh-Hurwitz Stability Criterion

1. It determines the stability but does not offer the method to stabilize an unstable system.
2. This method suits checking the stability of only linear systems.
3. The accurate position of the closed-loop poles in the s-plane is not determined.
4. It is applicable only when there is a characteristic equation having real coefficients.

This is all about checking the stability with the help of the Routh-Hurwitz stability criterion.