Root Locus in Control System

A graphical method used for analyzing the location and movement of poles in the s-plane with the variation in the gain factor of the system is known as Root Locus. This technique is used to check the stability of the closed-loop control system.

So, in simple terms, a graph plotted for roots of a characteristic equation by varying the system parameter (generally gain) from 0 to infinity is called Root Locus.

Root Locus Analysis was proposed by W R Evans in the year 1948.

Introduction

Previously we have seen that the roots of the characteristic equation are used to determine the stability of the closed-loop system. More specifically, the location of the closed-loop poles in the s-plane gives information about the stability of the closed-loop control system.

This clearly signifies that the nature of the transient response of the system shows dependency on the location of the poles in the s-plane. However, we all must know how the location of poles in s-plane varies with the variation in parameters of the system.

So, the root locus method helps to determine the movement of the poles in the s-plane with the variation in gain of the control system.

Concept of Root Locus

Suppose we have a closed-loop system as represented below:

For the above given closed-loop system, gain K is a variable parameter which is a part of the forward path of the system.

So, the transfer function for the above system will be given as:

We are already aware of the fact the characteristic equation of the closed-loop system is represented by equating the denominator of the transfer function to 0.

So, with the system gain K, the characteristic equation will be given as:

1 + KG(s)H(s) = 0

This shows that the roots of the characteristic equation given above now depends on the variable ‘K’.

So, this leads to taking us to the conclusion that if gain K is varied from – ∞ to + ∞ then every individual value of k within this range will provide a different set of locations of the poles in the s-plane.

Hence, root locus is defined as the locus of the poles of the closed-loop control system achieved for the various values of K ranging between – ∞ to + ∞. However, it is generally assumed to be between 0 to ∞.

Thus, the technique helps in determining the stability of the system and so is utilized as a stability criterion in control theory.

Angle and Magnitude Condition of Root Locus

The characteristic equation of a general closed-loop negative feedback system is given as:

1 + G(s)H(s) = 0

So,

G(s)H(s) = -1

As s-plane is complex in nature, constituting both real and imaginary value. Thus, writing the above equation as:

G(s)H(s) = -1 + j0

This means G(s)H(s) is also complex. Thus, the above-given equation must be satisfied for each individual value of s in order to be present on the root locus.

Further, the two conditions of root locus are:

1. Angle condition
2. Magnitude condition

Angle condition: As we know,

G(s)H(s) = -1 + j0

On equating angles, we will get,

∠G(s)H(s) = ± (2r + 1) 180°

: r = 0, 1, 2 —

It is to be noted here that – 1 + j0 = 1 ∠ ± 180°. However, – 1 + j0 will be present on the negative real axis of the s-plane.

Thus, can be traced as magnitude value 1 and ∠ ± 180°, ± 540°—– ± (2r + 1) 180°, as shown below.

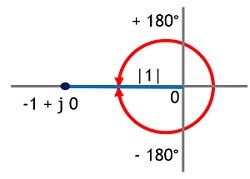
Hence, for the angle condition, ∠G(s)H(s) for any of the roots of the general characteristic equation will be ± (2r + 1) 180° i.e., odd multiples of 180°.

This signifies to be present on the root locus, the point must necessarily satisfy the angle condition. That means the calculated angle of G(s)H(s) at a point should be an odd multiple of ±180°.

Magnitude Condition: Further for the magnitude condition, the magnitude of both RHS and LHS must be equated for the equation G(s)H(s) = -1

Hence,

|G(s)H(s)| = |-1 + j0| = 1

It is to be noted that with the unknown value of K, we will not be able to determine |G(s)H(s)| at any point in s-plane. However, if we get an idea regarding the existence of a point in s-plane on the root locus then it must also satisfy the magnitude condition.

So, the value of K for a point whose presence on the root locus is obtained by the angle condition can be determined by the magnitude condition.

And the obtained value of K signifies the gain of the system for which a point on root locus acts as the root of the characteristic equation.

It is to be noted here that to apply the magnitude condition in order to get K, it is necessary that the existence of point on the root locus must be confirmed by the angle condition.

Advantages of Root Locus

• The locations of the poles provide the absolute stability of the system.
• Root locus helps to determine the value of gain of the system i.e., K for any specific location on the plot, using the magnitude condition.
• A system can be more precisely designed if K is determined for a specific damping ratio of the system.
• It helps in determining the gain margin and phase margin of the system.
• The root locus also helps in finding the information related to the settling time of the system.
• Its implementation is quite easy.
• By using the root locus technique, the overall performance of the system can be predicted.

So, here we have given an idea about the root locus. In the upcoming article, we will see how the root locus is constructed with example.