Stability of Control System

The stability of a control system is defined as the ability of any system to provide a bounded output when a bounded input is applied to it. More specifically, we can say, that stability allows the system to reach the steady-state and remain in that state for that particular input even after variation in the parameters of the system.

Stability is considered to be an important property of a control system. It is also referred as the system’s ability to reach the steady-state.

As it is an important characteristic thus the performance of the control system shows a high dependency on stability.

Introduction

We have already studied about the control system, that the various units of the control system combinedly operate so as to provide a specific output of the system.

In order to get the specified output, the various parameters of the system must be controlled. Along with this, the system must be stable enough so that the output must not get affected by the undesirable variations in the parameter of the system or disturbances.

Thus we can say that a stable system is designed so as to get the desired response of the system without any intolerable variation with the changes in the system parameters.

It is to be noted here that stability or instability is the characteristic property of the control system and thus depends on the closed-loop poles of the system.

Therefore, we can say that stability is a factor of the system which is independent of the input of the system. However, the steady-state output of the system is dependent on the poles of the applied input.

Stability of Control System

We have already discussed that a stable system generates bounded output for bounded input (BIBO).

Now the question arises what is bounded signal?

Bounded value of a signal represents a finite value. More specifically, we can say, the bounded signal holds a finite value of maxima and minima. Thus, if maxima and minima of any signal are finite then this means all the other values between maxima and minima will also be finite.

Suppose we have a signal shown below:

As we can see that here the maxima and minima of the signal represented above is having finite values. Thus such a signal is said to be bounded and if such an output is provided by a system then it is said to be a stable system.

Therefore, conversely, we can say that an unstable system provides an unbounded output when the applied input is bounded in nature.

Now, what are unbounded signals?

So, generally, the signals whose graph shows continuous rise thereby showing infinite value such as ramp signal are known as unbounded signals. The figure shown below represents the unbounded signal:

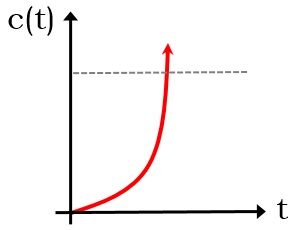
Sometimes we come across asymptotically stable systems which are defined as the systems whose output progresses 0, when the input is not present, even when the parameters of the system show variation.

It is to be noted here that poles of the transfer function, is a factor defining the stability of the control system.

Now the question arises, how poles can give information regarding the stability of the system?

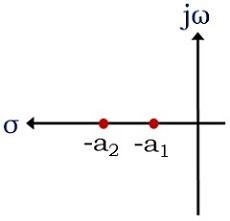
• When the poles of the transfer function of the system are located on the left side of the s-plane then it is said to be a stable system. However, as the poles progress towards 0 or origin, then, in this case, the stability of the system decreases.
  
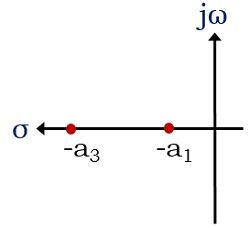
• Now there exist two conditions for the poles that are present in the imaginary axis:

1. If for a system, the poles are present in the imaginary axis and are non-repetitive in nature, then it is said to be a marginally stable system.
   
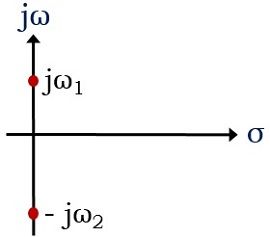
2. However, if there exist repetitive poles in the imaginary axis of the s-plane. Then it is called to be an unstable system.
   

• If a system having poles in the right domain of the s-plane, then such a system is called an unstable system. The presence of even a single pole in the right half makes the system unstable.
  
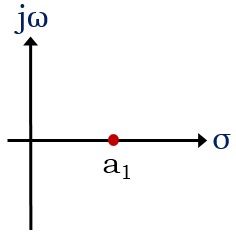
• The poles that are present close to the origin are said to be dominant poles. Thus if a stable system is having poles -a₁ and -a₂ then, then -a₁ is considered to the dominant pole of that particular system.
  

• A system is specifically considered to be an unstable system, if its output does not approach 0, thereby representing some value even in the absence of input.

Thus we can say that the position of the poles in the s-plane corresponds to the stability of the system.

Types of Stable System

• Absolutely stable system: An absolutely stable system is the one that provides bounded output even for the variation in the parameters of the system. This means it is such a system whose output after reaching a steady-state does not show changes irrespective of the disturbances or variation in the system parameter values.

The figure shown below represents the step response of an absolutely stable system:

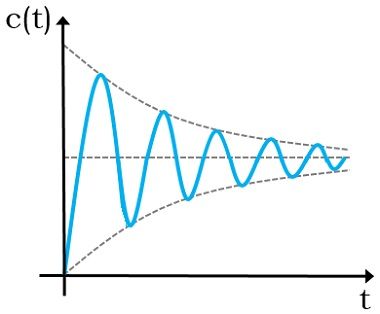
The nature of poles for the absolutely stable condition must be real and negative.

The figure below represents an unstable system:

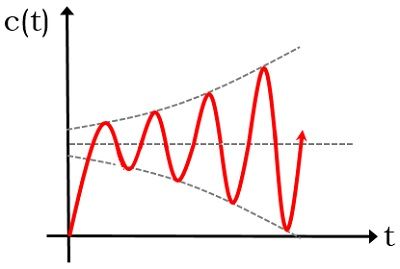
• Conditionally stable system: A conditionally stable system gives bounded output for the only specific conditions of the system that is defined by the parameter of the system.

Thus we can say here the system exhibits stability only under particular conditions.

And if that particular condition is violated then the system generates unbounded output.

• Marginally/ Critically stable system: A marginally stable system is the one that generates a signal which is oscillating with constant frequency and amplitude when a bounded input is provided to it.

These oscillations are known as sustained oscillations. The figure here represents the step response of a marginally stable system:

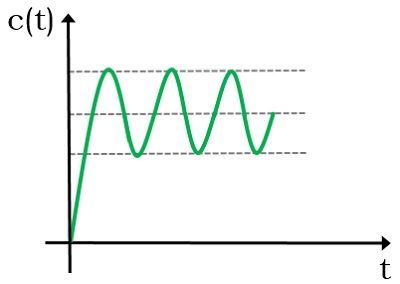
The nature of the closed-loop poles must be non-repetitive and located on the imaginary axis.

In this way, the stability of the control system is studied.